\[ \begin{equation} \left[ \begin{array}{c} 3 t^{2} - 2 t^{3} \\ 3 t - 3 t^{2} \\ \end{array} \right] \end{equation} \]
大学入試とJulia言語(JuliaTokai #21)
清水 団 Dan Shimizu (@dannchu)
2025-03-30
はじめに
自己紹介
- 清水 団(しみず・だん)
- 東京都板橋区 城北中学校・高等学校 に数学科の教員として勤務
- 2021年度より教頭です。
Julia言語のについて
Juliaは統計処理や科学技術計算、機械学習に強いプログラミング言語といわれています。 例えばStatsBase.jlやDistributions.jlなどのパッケージを使用すると、統計モデリングや仮説検定、回帰分析、時系列分析などの統計処理を行えます。
東京大(理系)2025・数学
2025年2月25日に行われた東京大学の入学試験の理系の数学の問題をJulia言語を用いて,「解く」というよりも「考えて」みました。コードを書くときはできるだけ,juliaのパッケージを利用しました。
また,quartoというパブリッシング・システムを用いてWebページを作成しました。基本Markdownで,コードの読み込みも容易です。今回は利用していませんが,新たな数式処理のtypstも実装可能です。
第1問
問題

julia言語
シンボリックパッケージ
Symbolics.jlを利用図示・積分・微分
- 図示は描画パッケージ
Plots.jlを利用 - 積分は数値積分パッケージ
QuadGK.jlを利用 - 微分は自動微分パッケージ
Zygote.jlを利用
- 図示は描画パッケージ
多項式パッケージ
Polynomials.jlを利用
using Symbolics
@variables t;
A,B,C,D = [0,0],[0,1],[1,1],[1,0];
f(X,Y,t) = (1-t)*X + t*Y
P(t) = f(A,B,t)
Q(t) = f(B,C,t)
R(t) = f(C,D,t)
S(t) = f(P(t),Q(t),t)
T(t) = f(Q(t),R(t),t)
U(t) = f(S(t),T(t),t)
expand.(U(t)) using Plots
plot(t->U(t)[1], t->U(t)[2], 0, 1,
aspectratio = true ,
line = 4, leg = false, fill = (0, :orange))(0.5999999999999999, 1.1102230246251565e-16)
l(a) = quadgk(t -> sqrt(x'(t)^2 + y'(t)^2) , 0, a)[1]
X =0:.05:1
Y = l.(X)
using Polynomials
println(fit(X,Y,1))
println(fit(X,Y,2))
println(fit(X,Y,3))
plot(fit(X,Y,1),xlim=(0,1),label="fit#3")
plot!(fit(X,Y,2),xlim=(0,1),label="fit#2")
plot!(fit(X,Y,3),xlim=(0,1),label="fit#3")
scatter!(X,Y,label="data") 0.0855 + 1.829*x
0.0855 + 1.829*x + 8.38226e-16*x^2
-1.66958e-16 + 3.0*x - 3.0*x^2 + 2.0*x^3第2問
問題
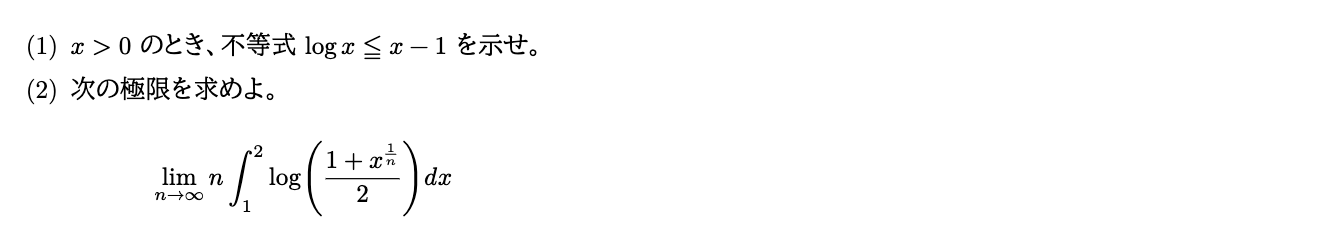
julia言語
- 描画パッケージ
Plots.jlを利用 - 数値積分パッケージ
QuadGK.jlを利用 - n=10^6くらいで計算してみる
f(10 ^ 6) = 0.19314720411554417
log(2) - 1 / 2 = 0.1931471805599453第3問
問題

julia言語
- 描画パッケージ
Plots.jlを利用(アニメーション) - 最小値パッケージ
Optim.jlを利用 - プリントパッケージ
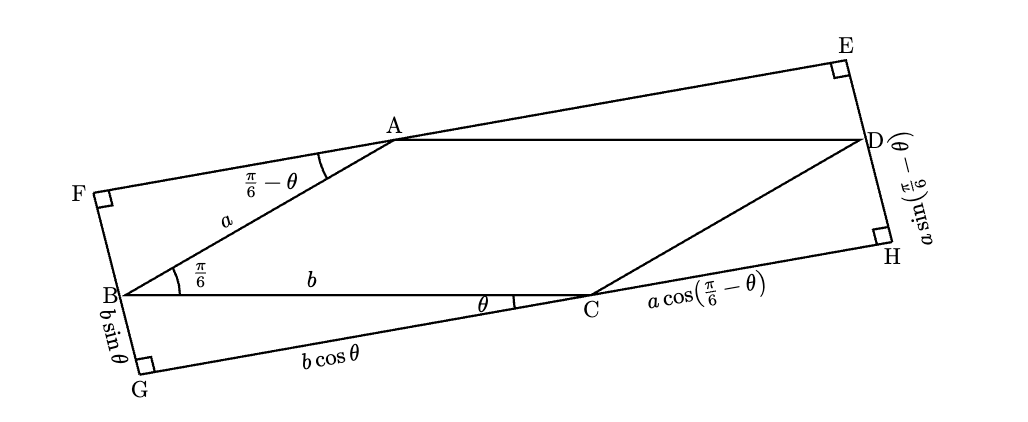
Printf.jlを利用 - 参考図(
typstで作成)![]()
using Plots
S(a,b,θ) = a*b*sin(π/6)+b^2 * sin(θ) * cos(θ)+a^2 * sin(π/6- θ)*cos(π/6- θ)
# アニメーションの作成
@gif for b in 1:0.005:2
plot(x -> S(1, b, x), 0, π/6, label =false,
title = "S(1, $(round(b,digits=1)), θ)", legend = :topright)
end every 1using Printf,Optim
# 関数 S(a, b, θ)
S(a, b, θ) = a*b*sin(π/6) + b^2 * sin(θ)*cos(θ) + a^2 * sin(π/6 - θ)*cos(π/6 - θ)
# θ ∈ [0, π/6] の範囲で最大値を求める関数
function max_S(a, b)
result = Optim.optimize(θ -> -S(a, b, θ), 0.0, π/6) # 最大化なのでマイナスを最小化
θ_max = Optim.minimizer(result)
S_max = S(a, b, θ_max)
return θ_max, S_max
end
# 各 a, b の組に対して計算
a = 1
b_list = [1+.1*i for i=0:10]
for b in b_list
θ, Sval = max_S(a, b)
@printf "a=1, b=%.4f → θ=%.4f, max S=%.6f\n" b θ Sval
enda=1, b=1.0000 → θ=0.2618, max S=1.000000
a=1, b=1.1000 → θ=0.3434, max S=1.109933
a=1, b=1.2000 → θ=0.4132, max S=1.239062
a=1, b=1.3000 → θ=0.4708, max S=1.385884
a=1, b=1.4000 → θ=0.5177, max S=1.548764
a=1, b=1.5000 → θ=0.5236, max S=1.724279
a=1, b=1.6000 → θ=0.5236, max S=1.908513
a=1, b=1.7000 → θ=0.5236, max S=2.101407
a=1, b=1.8000 → θ=0.5236, max S=2.302961
a=1, b=1.9000 → θ=0.5236, max S=2.513176
a=1, b=2.0000 → θ=0.5236, max S=2.732051b_list = [1.4+.01*i for i=0:10]
for b in b_list
θ, Sval = max_S(a, b)
@printf "a=1, b=%.4f → θ=%.4f, max S=%.6f\n" b θ Sval
enda=1, b=1.4000 → θ=0.5177, max S=1.548764
a=1, b=1.4100 → θ=0.5219, max S=1.565878
a=1, b=1.4200 → θ=0.5236, max S=1.583127
a=1, b=1.4300 → θ=0.5236, max S=1.600468
a=1, b=1.4400 → θ=0.5236, max S=1.617895
a=1, b=1.4500 → θ=0.5236, max S=1.635409
a=1, b=1.4600 → θ=0.5236, max S=1.653010
a=1, b=1.4700 → θ=0.5236, max S=1.670697
a=1, b=1.4800 → θ=0.5236, max S=1.688471
a=1, b=1.4900 → θ=0.5236, max S=1.706331
a=1, b=1.5000 → θ=0.5236, max S=1.724279第4問
問題

julia言語
- 素数パッケージ
Primes.jlを利用 - プリントパッケージ
Printf.jlを利用
using Primes
f(a::Int, x::Int) = x^2 + x - a
for a = 1:100 , n = 1:100
val = f(a, n)
if val ≥ 0 && isqrt(val)^2 == val
println("f($a, $n) = $val, $(n≤a) ")
end
endf(1, 1) = 1, true
f(2, 1) = 0, true
f(2, 2) = 4, true
f(3, 3) = 9, true
f(4, 4) = 16, true
f(5, 2) = 1, true
f(5, 5) = 25, true
f(6, 2) = 0, true
f(6, 6) = 36, true
f(7, 7) = 49, true
f(8, 3) = 4, true
f(8, 8) = 64, true
f(9, 9) = 81, true
f(10, 10) = 100, true
f(11, 3) = 1, true
f(11, 4) = 9, true
f(11, 11) = 121, true
f(12, 3) = 0, true
f(12, 12) = 144, true
f(13, 13) = 169, true
f(14, 5) = 16, true
f(14, 14) = 196, true
f(15, 15) = 225, true
f(16, 4) = 4, true
f(16, 16) = 256, true
f(17, 6) = 25, true
f(17, 17) = 289, true
f(18, 18) = 324, true
f(19, 4) = 1, true
f(19, 19) = 361, true
f(20, 4) = 0, true
f(20, 7) = 36, true
f(20, 20) = 400, true
f(21, 5) = 9, true
f(21, 21) = 441, true
f(22, 22) = 484, true
f(23, 8) = 49, true
f(23, 23) = 529, true
f(24, 24) = 576, true
f(25, 25) = 625, true
f(26, 5) = 4, true
f(26, 6) = 16, true
f(26, 9) = 64, true
f(26, 26) = 676, true
f(27, 27) = 729, true
f(28, 28) = 784, true
f(29, 5) = 1, true
f(29, 10) = 81, true
f(29, 29) = 841, true
f(30, 5) = 0, true
f(30, 30) = 900, true
f(31, 7) = 25, true
f(31, 31) = 961, true
f(32, 11) = 100, true
f(32, 32) = 1024, true
f(33, 6) = 9, true
f(33, 33) = 1089, true
f(34, 34) = 1156, true
f(35, 12) = 121, true
f(35, 35) = 1225, true
f(36, 8) = 36, true
f(36, 36) = 1296, true
f(37, 37) = 1369, true
f(38, 6) = 4, true
f(38, 13) = 144, true
f(38, 38) = 1444, true
f(39, 39) = 1521, true
f(40, 7) = 16, true
f(40, 40) = 1600, true
f(41, 6) = 1, true
f(41, 9) = 49, true
f(41, 14) = 169, true
f(41, 41) = 1681, true
f(42, 6) = 0, true
f(42, 42) = 1764, true
f(43, 43) = 1849, true
f(44, 15) = 196, true
f(44, 44) = 1936, true
f(45, 45) = 2025, true
f(46, 10) = 64, true
f(46, 46) = 2116, true
f(47, 7) = 9, true
f(47, 8) = 25, true
f(47, 16) = 225, true
f(47, 47) = 2209, true
f(48, 48) = 2304, true
f(49, 49) = 2401, true
f(50, 17) = 256, true
f(50, 50) = 2500, true
f(51, 11) = 81, true
f(51, 51) = 2601, true
f(52, 7) = 4, true
f(52, 52) = 2704, true
f(53, 18) = 289, true
f(53, 53) = 2809, true
f(54, 9) = 36, true
f(54, 54) = 2916, true
f(55, 7) = 1, true
f(55, 55) = 3025, true
f(56, 7) = 0, true
f(56, 8) = 16, true
f(56, 12) = 100, true
f(56, 19) = 324, true
f(56, 56) = 3136, true
f(57, 57) = 3249, true
f(58, 58) = 3364, true
f(59, 20) = 361, true
f(59, 59) = 3481, true
f(60, 60) = 3600, true
f(61, 10) = 49, true
f(61, 13) = 121, true
f(61, 61) = 3721, true
f(62, 21) = 400, true
f(62, 62) = 3844, true
f(63, 8) = 9, true
f(63, 63) = 3969, true
f(64, 64) = 4096, true
f(65, 9) = 25, true
f(65, 22) = 441, true
f(65, 65) = 4225, true
f(66, 14) = 144, true
f(66, 66) = 4356, true
f(67, 67) = 4489, true
f(68, 8) = 4, true
f(68, 11) = 64, true
f(68, 23) = 484, true
f(68, 68) = 4624, true
f(69, 69) = 4761, true
f(70, 70) = 4900, true
f(71, 8) = 1, true
f(71, 15) = 169, true
f(71, 24) = 529, true
f(71, 71) = 5041, true
f(72, 8) = 0, true
f(72, 72) = 5184, true
f(73, 73) = 5329, true
f(74, 9) = 16, true
f(74, 10) = 36, true
f(74, 25) = 576, true
f(74, 74) = 5476, true
f(75, 12) = 81, true
f(75, 75) = 5625, true
f(76, 16) = 196, true
f(76, 76) = 5776, true
f(77, 26) = 625, true
f(77, 77) = 5929, true
f(78, 78) = 6084, true
f(79, 79) = 6241, true
f(80, 27) = 676, true
f(80, 80) = 6400, true
f(81, 9) = 9, true
f(81, 17) = 225, true
f(81, 81) = 6561, true
f(82, 13) = 100, true
f(82, 82) = 6724, true
f(83, 11) = 49, true
f(83, 28) = 729, true
f(83, 83) = 6889, true
f(84, 84) = 7056, true
f(85, 10) = 25, true
f(85, 85) = 7225, true
f(86, 9) = 4, true
f(86, 18) = 256, true
f(86, 29) = 784, true
f(86, 86) = 7396, true
f(87, 87) = 7569, true
f(88, 88) = 7744, true
f(89, 9) = 1, true
f(89, 14) = 121, true
f(89, 30) = 841, true
f(89, 89) = 7921, true
f(90, 9) = 0, true
f(90, 90) = 8100, true
f(91, 19) = 289, true
f(91, 91) = 8281, true
f(92, 12) = 64, true
f(92, 31) = 900, true
f(92, 92) = 8464, true
f(93, 93) = 8649, true
f(94, 10) = 16, true
f(94, 94) = 8836, true
f(95, 32) = 961, true
f(95, 95) = 9025, true
f(96, 11) = 36, true
f(96, 15) = 144, true
f(96, 20) = 324, true
f(96, 96) = 9216, true
f(97, 97) = 9409, true
f(98, 33) = 1024, true
f(98, 98) = 9604, true
f(99, 99) = 9801, true
f(100, 100) = 10000, true using Primes,Printf
f(a::Int, x::Int) = x^2 + x - a
function N(a)
k = 0
for n = 1:a
val = f(a, n)
if val ≥ 0 && isqrt(val)^2 == val
k += 1
end
end
return k
end
println(" a | N(a) | 4a+1 | isprime?")
println("-----|------|------|----------")
for a = 1:120
count = N(a)
val = 4a + 1
is_p = count == 1 ? string(isprime(val)) : ""
@printf("%4d | %4d | %4d | %s\n", a, count, val, is_p)
end a | N(a) | 4a+1 | isprime?
-----|------|------|----------
1 | 1 | 5 | true
2 | 2 | 9 |
3 | 1 | 13 | true
4 | 1 | 17 | true
5 | 2 | 21 |
6 | 2 | 25 |
7 | 1 | 29 | true
8 | 2 | 33 |
9 | 1 | 37 | true
10 | 1 | 41 | true
11 | 3 | 45 |
12 | 2 | 49 |
13 | 1 | 53 | true
14 | 2 | 57 |
15 | 1 | 61 | true
16 | 2 | 65 |
17 | 2 | 69 |
18 | 1 | 73 | true
19 | 2 | 77 |
20 | 3 | 81 |
21 | 2 | 85 |
22 | 1 | 89 | true
23 | 2 | 93 |
24 | 1 | 97 | true
25 | 1 | 101 | true
26 | 4 | 105 |
27 | 1 | 109 | true
28 | 1 | 113 | true
29 | 3 | 117 |
30 | 2 | 121 |
31 | 2 | 125 |
32 | 2 | 129 |
33 | 2 | 133 |
34 | 1 | 137 | true
35 | 2 | 141 |
36 | 2 | 145 |
37 | 1 | 149 | true
38 | 3 | 153 |
39 | 1 | 157 | true
40 | 2 | 161 |
41 | 4 | 165 |
42 | 2 | 169 |
43 | 1 | 173 | true
44 | 2 | 177 |
45 | 1 | 181 | true
46 | 2 | 185 |
47 | 4 | 189 |
48 | 1 | 193 | true
49 | 1 | 197 | true
50 | 2 | 201 |
51 | 2 | 205 |
52 | 2 | 209 |
53 | 2 | 213 |
54 | 2 | 217 |
55 | 2 | 221 |
56 | 5 | 225 |
57 | 1 | 229 | true
58 | 1 | 233 | true
59 | 2 | 237 |
60 | 1 | 241 | true
61 | 3 | 245 |
62 | 2 | 249 |
63 | 2 | 253 |
64 | 1 | 257 | true
65 | 3 | 261 |
66 | 2 | 265 |
67 | 1 | 269 | true
68 | 4 | 273 |
69 | 1 | 277 | true
70 | 1 | 281 | true
71 | 4 | 285 |
72 | 2 | 289 |
73 | 1 | 293 | true
74 | 4 | 297 |
75 | 2 | 301 |
76 | 2 | 305 |
77 | 2 | 309 |
78 | 1 | 313 | true
79 | 1 | 317 | true
80 | 2 | 321 |
81 | 3 | 325 |
82 | 2 | 329 |
83 | 3 | 333 |
84 | 1 | 337 | true
85 | 2 | 341 |
86 | 4 | 345 |
87 | 1 | 349 | true
88 | 1 | 353 | true
89 | 4 | 357 |
90 | 2 | 361 |
91 | 2 | 365 |
92 | 3 | 369 |
93 | 1 | 373 | true
94 | 2 | 377 |
95 | 2 | 381 |
96 | 4 | 385 |
97 | 1 | 389 | true
98 | 2 | 393 |
99 | 1 | 397 | true
100 | 1 | 401 | true
101 | 5 | 405 |
102 | 1 | 409 | true
103 | 2 | 413 |
104 | 2 | 417 |
105 | 1 | 421 | true
106 | 3 | 425 |
107 | 4 | 429 |
108 | 1 | 433 | true
109 | 2 | 437 |
110 | 5 | 441 |
111 | 2 | 445 |
112 | 1 | 449 | true
113 | 2 | 453 |
114 | 1 | 457 | true
115 | 1 | 461 | true
116 | 4 | 465 |
117 | 2 | 469 |
118 | 2 | 473 |
119 | 3 | 477 |
120 | 2 | 481 | 第5問
問題

julia言語
- 組み合わせパッケージ
Combinatorics.jlを利用
using Combinatorics
# 操作 T_i: i番目とi+1番目の値を比較し、左の方が大きければ入れ替える
function apply_T!(perm, i)
if perm[i] > perm[i + 1]
perm[i], perm[i + 1] = perm[i + 1], perm[i]
end
end
# 1回の操作ループ:T₁~Tₙ₋₁ → Tₙ₋₁~T₁
function perform_all_T!(perm)
n = length(perm)
for i in 1:n-1
apply_T!(perm, i)
end
for i in n-1:-1:1
apply_T!(perm, i)
end
end
# 並べ替え後に昇順になる初期順列を全て集める
function valid_permutations(n)
target = collect(1:n)
results = []
for perm in permutations(1:n)
temp = collect(perm)
perform_all_T!(temp)
if temp == target
push!(results, perm)
end
end
return results
end
# 実行例:n = 4 のとき
valid_permutations(4)20-element Vector{Any}:
[1, 2, 3, 4]
[1, 2, 4, 3]
[1, 3, 2, 4]
[1, 3, 4, 2]
[1, 4, 2, 3]
[1, 4, 3, 2]
[2, 1, 3, 4]
[2, 1, 4, 3]
[2, 3, 1, 4]
[2, 3, 4, 1]
[2, 4, 1, 3]
[2, 4, 3, 1]
[3, 1, 2, 4]
[3, 1, 4, 2]
[3, 2, 1, 4]
[3, 2, 4, 1]
[4, 1, 2, 3]
[4, 1, 3, 2]
[4, 2, 1, 3]
[4, 2, 3, 1]1
2
6
20
68
232
792
2704
9232
31520第6問
問題

julia言語
- 描画パッケージ
Plots.jlを利用 - 境界で最大・最小を取るのかな。
using Plots
# 曲線C上の点を生成(z such that |z - 1/2| = 1/2)
function generate_C(N=500)
θ = range(0, 2π, length=N)
return [1/2 + 1/2 * cis(t) for t in θ if abs(1/2 + 1/2 * cis(t)) > 1e-6] # 原点を除く
end
plot(1 ./generate_C(),aspectratio=true,
xlim=(-2,2),ylim=(-2,2),label="1/z",legend=false)
# (2) α ≠ β に対して 1/α^2 + 1/β^2 のとる範囲を図示
function plot_sum_inv_squares()
C = generate_C(10^3)
points = ComplexF64[]
for _ = 1:10^5
α, β = rand(C), rand(C)
push!(points, 1/α^2 + 1/β^2)
end
scatter(points,aspectratio=true,
xlim=(-3,3),ylim=(-3,3),)
end
plot_sum_inv_squares()# (3) C上にない点を使って Re(1/γ) の最大・最小を求める
# まあ,境界でmax,minを取るとしましょう。
C = generate_C(1000)
f(z) = 2/z^2
points = f.(C)
w = 1 ./ points
println("(3) Re(1/γ) の最大:", maximum(real.(w)))
println("(3) Re(1/γ) の最小:", minimum(real.(w)))
plot(w,aspectratio=true,label="1/γ")(3) Re(1/γ) の最大:0.5
(3) Re(1/γ) の最小:-0.06250000000000001